Spider Traps 及平滑措置

可以预见，如果把真实的 Web 组织成转移矩阵，那么这将是一个极其稀疏的矩阵，从矩阵论知识可以推断，极端稀疏的转移矩阵迭代相乘可能会使得向量v变得很是不服滑，即一些节点拥有很年夜的 rank，而年夜大都节点 rank 值接近0。而一种叫做 Spider Traps 节点的存在加重了这种不服滑。例如下图：

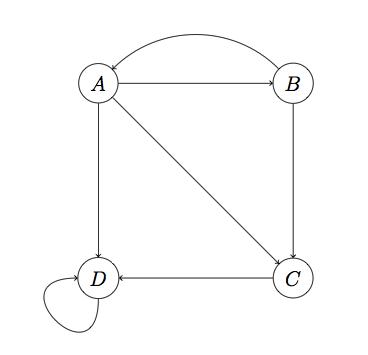
D 有外链所以不是 Dead Ends，可是它只链向自己（注意链向自己也算外链，当然同时也是个内链）。这种节点叫做 Spider Trap，如果对这个图进行计较，会发现D的 rank 越来越年夜趋近于1，而其它节点 rank 值几近归零。

为了降服这种由于矩阵稀疏性和 Spider Traps 带来的问题，需要对 PageRank 计较体例进行一个平滑措置，具体做法是插手"心灵转移（teleporting）"。所谓心灵转移，就是我们认为在任何一个页面阅读的用户都有可能以一个极小的概率瞬间转移到别的一个随机页面。当然，这两个页面可能不存在超链接，因此不成能真的直接转移曩昔，心灵转移只是为了算法需要而强加的一种纯数学意义的概率数字。

插手心灵转移后，向量迭代公式变成：

其中β往往被设置为一个比较小的参数（0.2或更小），e为N维单位向量，插手e的原因是这个公式的前半部分是向量，因此必须将β/N转为向量才能相加。这样，整个计较就变得平滑，因为每次迭代的成果除依赖转移矩阵外，还依赖一个小概率的心灵转移。

以上图为例，转移矩阵M为：

设β为0.2，则加权后的M为：

因此：

如果按这个公式迭代算下去，会发现 Spider Traps 的效应被抑制了，从而每个页面都拥有一个公道的 pagerank。

Topic-Sensitive PageRank

其实上面的讨论我们躲避了一个事实，那就是"网页重要性"其实没一个标准谜底，对不合的用户，甚至有很年夜的不同。例如，当搜索"苹果"时，一个数码欢愉喜爱者多是想要看 iphone 的信息，一个果农多是想看苹果的代价走势和种植技能，而一个小朋友可能在找苹果的简笔划。抱负情况下，应该为每个用户维护一套专用向量，但面对海量用户这种体例显然不成行。所以搜索引擎一般会选择一种称为 Topic-Sensitive 的折中方案。Topic-Sensitive PageRank 的做法是预定义几个话题种别，例如体育、娱乐、科技等等，为每个话题伶仃维护一个向量，然后想体例关联用户的话题倾向，按照用户的话题倾向排序成果。

Topic-Sensitive PageRank 分为以下几步：

1、确定话题分类。

一般来讲，可以参考 Open Directory（DMOZ）的一级话题种别作为 topic。目前 DMOZ 的一级 topic 有：Arts（艺术）、Business（商务）、Computers（计较机）、Games（游戏）、Health（医疗健康）、Home（居家）、Kids and Teens（儿童）、News（新闻）、Recreation（娱乐修养）、Reference（参考）、Regional（地区）、Science（科技）、Shopping（购物）、Society（人文社会）、Sports（体育）。