简单 PageRank 计较

首先，我们将Web 做如下抽象：1、将每个网页抽象成一个节点；2、如果一个页面A有链接直接链向B，则存在一条有向边从A到B（多个相同链接不重复计较边）。因此，整个 Web 被抽象为一张有向图。

现在假定世界上只有四张网页：A、B、C、D，其抽象布局如下图：

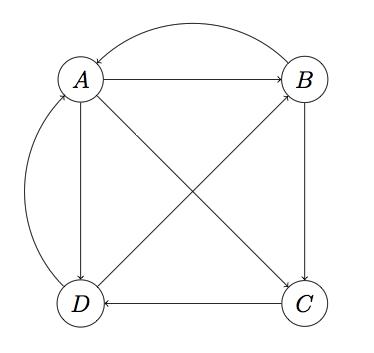
显然这个图是强连通的（从任一节点解缆都可以达到别的任何一个节点）。

然后需要用一种适合的数据布局暗示页面间的毗连关系。其实，PageRank 算法是基于这样一种布景思想：被用户拜候越多的网页更可能质量越高，而用户在阅读网页时主要通过超链接进行页面跳转，因此我们需要通过阐发超链接组成的拓扑布局来推算每个网页被拜候频率的凹凸。最简单的，我们可以假定当一个用户停留在某页面时，跳转到页面上每个被链页面的概率是相同的。例如，上图中A页面链向B、C、D，所以一个用户从A跳转到B、C、D的概率各为1/3。设一共有N个网页，则可以组织这样一个N维矩阵：其中i行j列的值暗示用户从页面j转到页面i的概率。这样一个矩阵叫做转移矩阵（Transition Matrix）。下面的转移矩阵M对应上图：

然后，设初始时每个页面的 rank 值为1/N，这里就是1/4。按A-D顺序将页面 rank 为向量v：

注意，M第一行别离是A、B、C和D转移到页面A的概率，而v的第一列别离是A、B、C和D当前的 rank，因此用M的第一行乘以v的第一列，所得成果就是页面A最新 rank 的公道估计，同理，Mv 的成果就别离代表A、B、C、D新 rank：

然后用M再乘以这个新的 rank 向量，又会产生一个更新的 rank 向量。迭代这个过程，可以证明v最终会收敛，即v约等于 Mv，此时计较停止。最终的v就是各个页面的 pagerank 值。例如上面的向量颠末几步迭代后，年夜约收敛在（1/4, 1/4, 1/5, 1/4），这就是A、B、C、D最后的 pagerank。

措置 Dead Ends

上面的 PageRank 计较体例假定 Web 是强连通的，但实际上，Web 其实不是强连通（甚至不是联通的）。下面看看 PageRank 算法如何措置一种叫做 Dead Ends 的情况。

所谓 Dead Ends，就是这样一类节点：它们不存在外链。看下面的图：

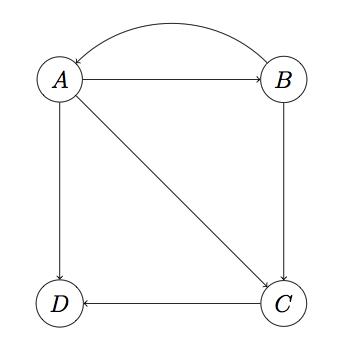
注意这里D页面不存在外链，是一个 Dead End。上面的算法之所以能成功收敛到非零值，很年夜水平依赖转移矩阵这样一个性质：每列的加和为1。而在这个图中，M第四列将全为0。在没有 Dead Ends 的情况下，每次迭代后向量v各项的和始终保持为1，而有了 Dead Ends，迭代成果将最终归零（要诠释为什么会这样，需要一些矩阵论的知识，比较死板，此处略）。

措置 Dead Ends 的体例如下：迭代拿失落图中的 Dead Ends 节点及 Dead Ends 节点相关的边（之所以迭代拿失落是因为当目前的 Dead Ends 被拿失掉队，可能会呈现一批新的 Dead Ends），直到图中没有 Dead Ends。对剩下部分计较 rank，然后以拿失落 Dead Ends 逆向顺序反推 Dead Ends 的 rank。

以上图为例，首先拿到D和D相关的边，D被拿到后，C就酿成了一个新的 Dead Ends，于是拿失落C，最终只剩A、B。此时可很容易算出A、B的 PageRank 均为1/2。然后我们需要反推 Dead Ends 的 rank，最后被拿失落的是C，可以看到C前置节点有A和B，而A和B的出度别离为 3 和2，因此C的 rank 为：1/2 * 1/3 + 1/2 * 1/2 = 5/12；最后，D的 rank 为：1/2 * 1/3 + 5/12 * 1 = 7/12。所以最终的 PageRank 为（1/2, 1/2, 5/12, 7/12）。